HowTo/Use Superelevation with Trainz 22
Contents |
What is superelevation in Trainz 22?
The "superelevation" or the slope of rails in curves is proposed since T:ANE (see this page : HowTo/Use Superelevation with Trainz 19 and T:ANE). This page updates the instructions for Trainz 22
To resist centrifugal force and and not to wear out prematurely the outer rail, the track must be tilted on bends.
Applying a gradient to a curved section of track is called superelevation.
Here is the example of a machine launched to 80 kph in a curve of 500 meters of beam. The slope of the track has been set to 4 °.

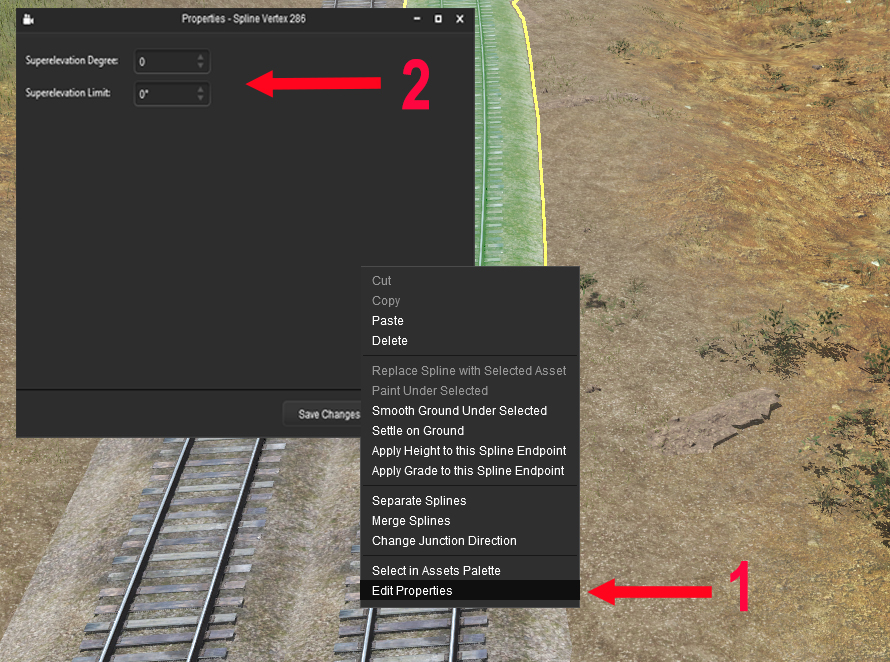
To implement Superelevation in Trainz 22, follow the steps below :
| On the tools palette,select the highlighted icone as shown on the opposite picture (1)
Clic on the track to select it (2) Clic on one of the submits of the selected track (3) |  |
Surperelevation : theoritical base
Everything that follows in this section is designed to give you the theoretical basis for calculating a superelevation.
In the next section, a spreadsheet will be provided to do all the calculations for you.
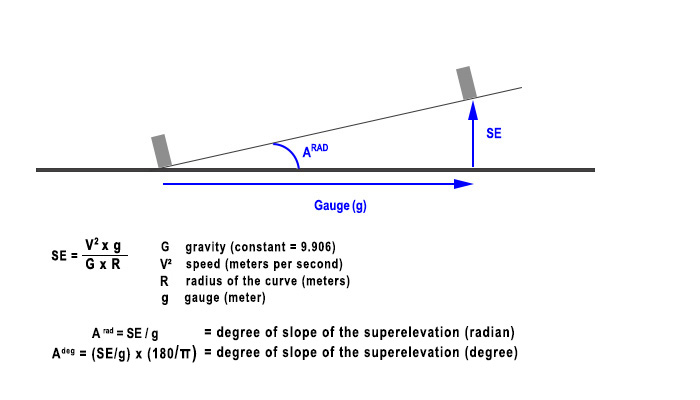
- The Superelevation (SE) is the height that the outside rail takes compared with the internal rail in a curve.
It is calculated as the diagram below shows it:
- Of the four variables above (G, V, R,g), one is unknown at start: the radius of the curve.
The diagram below shows how to determine it :
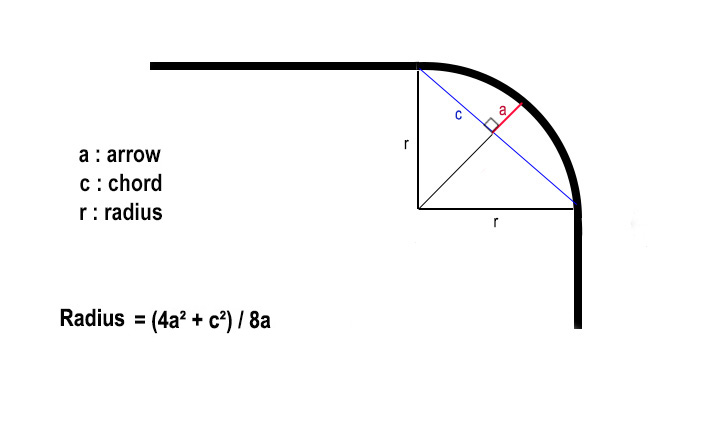
- Trainz 22 introduces an aditionnal concept for determining the superelevation of a curve: the degree of curvature.
| Here, with a quarter-circle curve, the curve angle is 90°.
With a chord of a given length : | 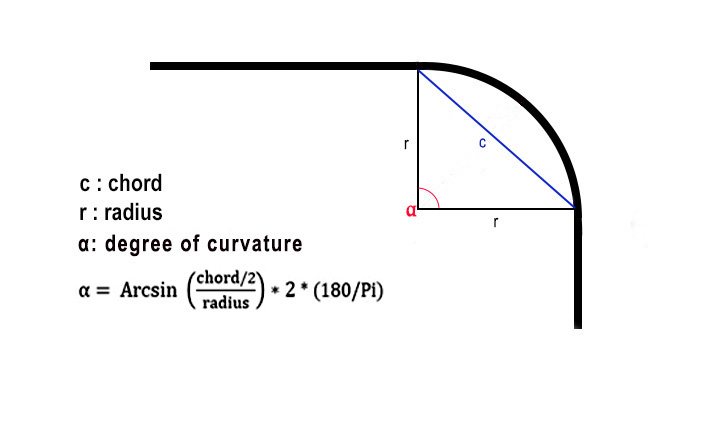 |
|
The parameter 'Superelevation Degree' is depicted in the game as : the degree of superelevation of this track vertex (where 0 is none, and 1 is one degree bank per degree of curvature). |
Superelevation: how do we go about it?
To proceed to the calculations, download and save to your hard drive the spreadsheet Here
Proceed in two steps :
- measure the chord and arrow of your curve
- proceed to the calculations with the spreadsheet
Measure the chord and arrow of your curve :
| In your Asset Pallet, select the spline 'ruler' <kuid:447125:108> Ruler Metric or <kuid:447125:109> Ruler Imperial
Measure the lengths of the chord and the arrow as shown opposite | 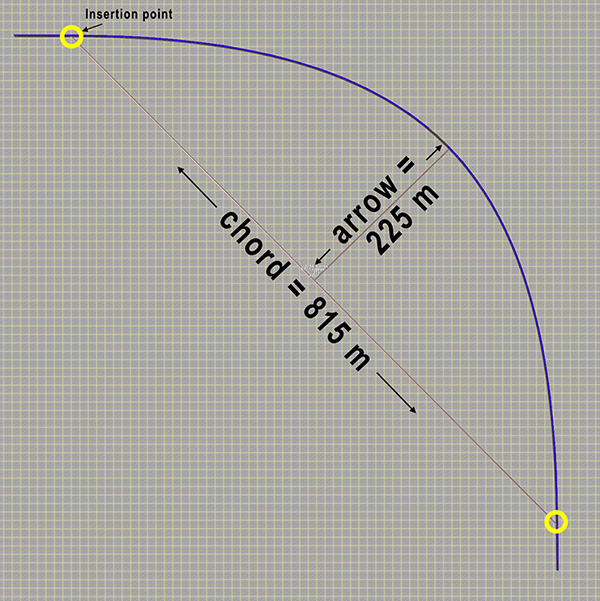 |
Procced to the calculations whith the spreadsheet :
For those who are curious...
The spreadsheet is based on the following observations:
- Calculating the gradient of curved track depends on the chord of the curve and the speed at which the train is travelling.
- As described in the precedent section 'Surperelevation : theoritical base', the gradient (in degree) of a curved track may be calculated quite easely ; but how do we translate this degree slope into Superelevatioon Degreee, a variable specific to Trainz?
- In Trainz, with the observation of a curve with a chord = 200 metres and an angle = 90°, we determine that there is a constant multiplier between the slope of the curve required and the Superelevation Degree value entered in Trainz.
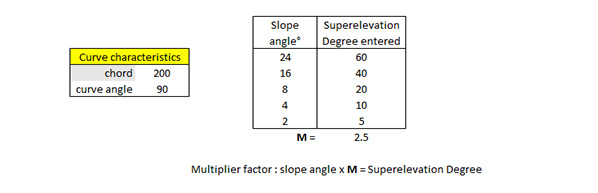
|
- Other observation : the coefficient M will apply to any curve of chord = 200 metres, whatever the angle of this curve.
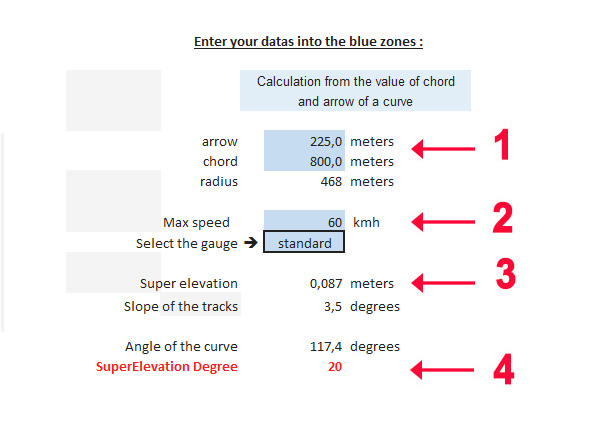
Example: for a 90° bend with a chord length of 200 metres and a required slope angle of 8°, we calculate a SuperElevation Degree = 20 (as shown in the table above).
if this same bend were to be transformed to have an angle of 45°, the SuperElevation Degree = 20 value would still apply to produce in Trainz a bank angle of 4.3°, which correspond to the desired value.
- And now, how can we calculate the superelevation degree if we change the chord of our curve?
As before, there is a relationship between the multiplier M and the length of the chord. This establishes the variable Mchord.
This relationship follows a polynomial equation of degree 2, as shown below:
| For a 90° curve : | 
|
- And this is how the spreadsheet works.
Once the values have been entered in the blue zones (arrow, chord and speed), the spreadsheet calculates the curve angle, the superelevation and the slope angle.
It then takes these elements and recalculates them as if the curve angle were 90° :
- it keeps the same value for the chord, but as the curve angle has changed, a new value of the radius of the curve is calculated
- according to the new value of the radius and the max speed of the train (as entered in the blue zone), it computes the slope angle of the track
- the variable Mchord is then determined from the chord value of the curve (the one entered in the blue zone and according to the formula in the graph above)
- Superelevation Degree = slope angle of the track x Mchord.
And if you're really very, very curious, you can see how it works directly in the spreadsheet : on the 'English(metric)' sheet, remove the sheet protection, restore column display and unmask the H:K columns.